![]() Nel suo libro "Liber abaci" Fibonacci espone il seguente problema:
Nel suo libro "Liber abaci" Fibonacci espone il seguente problema:
Un uomo possiede una coppia di conigli.
Quante coppie di conigli possono essere prodotte dalla coppia iniziale in un anno, supponendo che ogni mese, ogni coppia produca una nuova coppia in grado di riprodursi a sua volta dal secondo mese?
Lo abbiamo rappresentato insieme alla lavagna e sul quaderno...
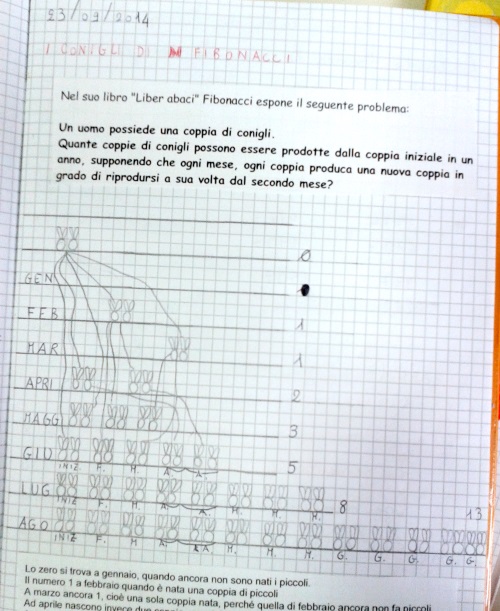
Lo zero si trova a gennaio, quando ancora non sono nati i piccoli.
Il numero 1 a febbraio quando è nata una coppia di piccoli
A marzo ancora 1, cioè una sola coppia nata, perché quella di febbraio ancora non fa piccoli
Ad aprile nascono invece due coppie, una dei conigli iniziale, l'altra della coppia di febbraio
A maggio sono nate tre coppie di piccoli: ora anche la coppia nata in marzo ha avuto due piccoli)
A giugno cinque coppie: una dalla coppia iniziale, e una ciascuna dalle coppie nate a febbraio, marzo e aprile.
Poi si aumenta più in fretta...
Ben presto i bambini hanno capito il meccanismo... e scoperto la regola della sequenza di Fibonacci (ogni numero della sequenza è la somma dei due precedenti).
0 - 1 - 1 - 2 - 3 - 5 - 8 - 13 - 21 - 44 - 63 - ...
Il lavoro ci ha permesso di contare velocemente fino a numeri grandi (e togliere un po' di ruggine estiva), di ripassare il valore posizionale delle cifre ed introdurre il periodo dei milioni e dei miliardi.





 Instagram - Schoolmate
Instagram - Schoolmate Twitter - ClassiDigitali
Twitter - ClassiDigitali